SOLUTION: The line joining the points (2,1) and (5,-8) is trisectedat the points P and Q. If the point P lies on the line 2x-y+k=0, find the value of k.

Algebra ->  Length-and-distance -> SOLUTION: The line joining the points (2,1) and (5,-8) is trisectedat the points P and Q. If the point P lies on the line 2x-y+k=0, find the value of k.       Log On


   

Question 1011414: The line joining the points (2,1) and (5,-8) is trisectedat the points P and Q. If the point P lies on the line 2x-y+k=0, find the value of k.
Answer by josgarithmetic(39621) About Me  (Show Source):
You can put this solution on YOUR website!
Outline of the process:
(1) Distance between the two points
(2) Equation of the line with the points
(3) Equation for the description, one-third the distance from either point
(4) Solve the equation to find the unknown coordinate matching the description

One-third the distance from (2,1) to (5,8):

Their distance sqrt%28%285-2%29%5E2%2B%288-1%29%5E2%29=highlight_green%28sqrt%2858%29%29

m=%288-1%29%2F%285-2%29=7%2F3
y-1=%287%2F3%29%28x-2%29
highlight_green%28y=%287%2F3%29x%2B1%2F3%29, the general point (x, (7/3)x+1/3).

Point P is one-third distance from (2,1) to (5,8), here making (2,1) the choice for reference
to start from.
sqrt%28%28x-2%29%5E2%2B%287x%2F3%2B1%2F3-1%29%5E2%29=%281%2F3%29sqrt%2858%29
---some algebra steps---
%28x-2%29%5E2%2B%287x%2F3-1%2F3%29%5E2=58%2F9
--work through some more steps--
highlight_green%2829x%5E2-32x-9=0%29
-
x=%2832-32%29%2F58=0 OR x=64%2F58=32%2F29

y-coordinate which properly fits would be, if checking with a sketched graph, is based on x=32%2F29.
y=7x%2F3%2B1%2F3
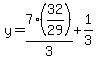
y=7%2832%2F29%29%2F3%2B1%2F3
highlight_green%28y=253%2F87%29

Point P is the point highlight%28x=32%2F29%29 and highlight%28y=253%2F87%29.

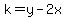
The question asked to find k, in the line containing P, being 2x-y%2Bk=0
k=y-2x
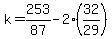
k=253%2F87-2%2832%2F29%29
highlight%28highlight%28highlight_green%28k=61%2F87%29%29%29