Question 1011396: A right triangle has legs 4 cm and 3cm. How far from the vertex must this triangle be cut by a line parallel to the longer diagonal so that:
(a) the area of the small right triangle will be equal to the area of the trapezoid formed
(b) the perimeter of the small triangle is equal to the perimeter of the trapezoid
Answer by josgarithmetic(39620)   (Show Source):
You can put this solution on YOUR website! A good set of pictures is necessary to do this right but, if k is the distance from hypotenuse to the base of the smaller triangle-hypotenuse,, then eventually you might be able to derive  . k is to be the distance between the two bases.
Part of that came from finding altitude of the original right triangle, from the "vertex" right angle to the hypotenuse, which found to be  , this altitude. The smaller triangle formed of half the original area is similar to the original given triangle, so sides are in proportion.
Not finished solving, but looking for k (to get from that above quadratic equation.)
---
STEPS
Hypotenuse base, 
There is a theorem about altitude for right triangle but not recalling it, resorting to
some basic trigonometry for sine.
 and  .
Altitude for smaller triangle is  .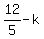
Original triangle's area (the larger, given) is  .
Smaller triangle and main given triangle are similar, and therefore linear parts are in proportion.
RATIO of small lengths to main lengths is  .
Base for the smaller triangle becomes  .
WANT smaller triangle area to be HALF the main triangle area.
Simplify this,... to obtain
-
Using formula for the general solution of a quadratic equation leads to
 and the MINUS form will be what is needed.
Note very carefully this k value is for the distance FROM the main triangle base toward the "vertex"
so some adjustment to YOUR answer is needed.
In either way, you will want to check that this found k value works. I did check but do not
include the check in this solution post.
|
|
|
