|
Question 1011308: Natalie performs a chemistry experiment where she records the temperature of an ongoing reaction. The solution is 93.5 degree C after 3 min.; 90 degree C after 5 min.;84.8 degree C after 9 min.;70.2 degree C after 18 min.; 54.4 degree after 30 min.; 42.5 degree C after 37 min.; and 24.9 degree C after 48 min. Perform a linear regression on this data to complete the following
what does the value of the correlation coefficient tell you about the correlation of the data?
write the equation of the best fitting line.
on average how much does the temperature decrease every 5 min.
If Natalie's solution is expected to freeze at -7 degrees C, how many minutes into the experiment should the solution freeze?
Thank you
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! What is expected as "Perform a linear regression on this data" depends on your course/book/teacher.
Before calculators (yes, I am that old),
we would do a lot of pencil and paper calculations,
using complicated formulas.
Maybe you are expected to use the functions in your calculator.
Those function uses formulas you do not need to remember,
to calculate results such as
correlation coefficient,
slope, and
y-intercept
of the linear regression best fit line.
Since I am sitting in front of my computer,
I would use the spreadsheet program I have installed (Microsoft Excel)
to tabulate, graph, and calculate the needed results.
My tabulation, graph and results look like this:
 
correlation coefficient:  (rounded to the first decimal place that is not a 9),
slope:  (rounded to 5 decimal places),
y-intercept:  (rounded to 4 decimal places),
best fit line (y=mx+b):  .
The absolute value of the correlation coefficient is very close to exactly  ,
and that means that the line fits the data very closely (as we see in the graph),
meaning that the linear model is right (that the temperature varies linearly with time).
The fact that the correlation coefficient is negative
shows that temperature decreases with time.
The slope tells us that the temperature decreases 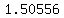 degrees per minute,
so on average, the temperature decreases   degrees (rounded) every  minutes.
The data allows us to predict temperature between 3 and 48 minutes,
but we may feel somewhat confident that the relationship still holds for
values of  (seconds) close to the edges of the [3,48] interval.
That is why I extended the best fit line in the graph to cover [0,68].
The line seems to cross the  x-axis at  (65 minutes).
We can solve the linear best fit equation for the time when  , and the solution freezes.
 ---> ---> ---> (rounded).
Since Natalie was measuring the time in whole minutes,
we can report the time the solution freezes with the same precision as  .
|
|
|
| |
