Question 1011204: The motor of a small boat produces a speed of 2 mph in still water. The boat is travelling in flowing water with a current velocity given by (-2, -1 ) . In what direction should the boat head to travel due east? (Represent the direction with a unit vector.)
Please show your work \ explain your answer
Found 2 solutions by stanbon, KMST:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! The motor of a small boat produces a speed of 2 mph in still water. The boat is travelling in flowing water with a current velocity given by (-2, -1 ) . In what direction should the boat head to travel due east? (Represent the direction with a unit vector.)
I'm assuming that velocity
-------
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! If this is the situation,
 , with the blue (-2,1) vector representing current velocity in mph,
and the green vectors representing its southward and westward components,
you would need the black vectors to neutralize the southward and westward pulls of the current.
As those black vectors add to a vector with magnitude greater than  , ,
there is no way that a small boat capable of only 2 mph in still water could move East.
At most you could neutralize some of the westward and all of the southward pull of the current,
and just drift West.
If the resultant velocity of the boat as seen by any observer on the river bank were along an East-West direction,
it would be (x[R],0).
The boat's velocity, (2cos(A),2sin(A)) with respect to the water
(as it would be if there was no current,
would have magnitude of ,
and would form an angle  measured clockwise from the positive x-axis.
That angle would be the direction the boat is heading .
The unit vector describing that direction is, of course,
     .
The boat's velocity as it would be in still water,
plus the velocity of the current add up to
the resultant velocity describing how the boat is moving respect to any observer on the river bank:
(-2,-1) + (2cos(A),2sin(A)) = (2cos(A)-2,2sin(A)-1)=(x[R],0) , meaning
 --->
As 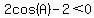 , the boat will drift West.
There is no way to go East.
For the boat to go an an East_west trajectory, we need
 ---> --->---> .
If we choose  , the unit vector is   , or approximately   ;
 ,
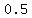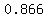and the boat will move East at that velocity  ,
meaning that it will go West at a speed of 0.27 mph.
If we choose  ,  ,
and the boat will move East at that velocity  ,
meaning that it will go West at a speed of 3.73 mph.
|
|
|
