Question 1011125: what is the length of the longest pole that can be put into a room of dimensions 10m×10m×5m. also find the volume of the pole if its radius is 70cm
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The room, with the pole, 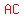 , ,
and the pole's shadow, 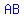 , would look like this: , would look like this:
 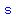 =length of AB, and =length of AB, and 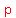 =length of AB, both in meters. =length of AB, both in meters.
On the floor of the room, 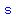 is the diagonal of a 10m×10m square is the diagonal of a 10m×10m square
(or the hypotenuse of a right triangle with legs measuring 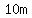 , ,
so the Pythagorean theorem tells us that
 . .
On an imaginary vertical plane, triangle  is a right triangle, is a right triangle,
and its legs' length, in meters, are
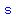 and and  . .
So the length, in meters, of hypotenuse  is is
 . .
That is the length of the longest pole that can be put into a room of dimensions 10m×10m×5m,
provided that the pole is pencil-thin or thinner.
If the pole is wider than pencil-thin its ends will not go all the way into corners  and and  , = , =
so it would need to be a bit shorter,
but I do not think that you are expected to do real world calculations,
as an engineer would do,
so the expected answer to the second question is the volume of a pole/cylinder
that is 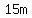 long and long and  in radius. in radius.
For a cylinder of radius  and height and height  , the volume is , the volume is
 , ,
so for your problem, the volume of the pole in cubic meters is
 . .
That is about  . .
|
|
|