Question 1011123: A small square is cut out of a larger square.
The side lengths of both squares, in centimetres, are whole numbers less than 25. The remaining area of the larger square is 57 square cm.
What is the perimeter of the small square in centimetres?
Solution: 32 cm
Can you show the work please. Thank you!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  = side length of the smaller square, in cm, = side length of the smaller square, in cm,
 = side length of the larger square, in cm, = side length of the larger square, in cm,
and 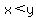 , of course. , of course.
So,
 = area of the smaller square, in square cm; = area of the smaller square, in square cm;
 = original area of the larger square, in square cm, and = original area of the larger square, in square cm, and
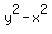 = remaining area of the larger square, in square cm. = remaining area of the larger square, in square cm.
The problem tells us that  , ,
and that  and and  are positive integers less than 25. are positive integers less than 25.
Algebra tells us that
 <--> <--> . .
Since  and and  are positive integers less than are positive integers less than  , with , with 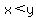 and and  are positive integers, and are positive integers, and
 . .
What positive integers less than  could be could be 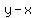 and and  ? ?
As 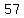 does not have too many factors, we can only write it as two products of positive integers: does not have too many factors, we can only write it as two products of positive integers:
 and and  . .
Only one of thpose products has both factors less than  . .
So,  ----> ----> . .
The perimeter of the small square in centimetres is
 . .
|
|
|