Question 1010946: John purchases an office complex that contains 150 offices. Records show that in a recession year only 70% of the offices are rented. John needs at least 110 offices to be rented to breakeven. John has asked you to determine, what is the probability John will breakeven this recession?
Answer by mathmate(429)   (Show Source):
You can put this solution on YOUR website!
Question:
John purchases an office complex that contains 150 offices. Records show that in a recession year only 70% of the offices are rented. John needs at least 110 offices to be rented to breakeven. John has asked you to determine, what is the probability John will breakeven this recession?
Solution:
This problem can be solved using the binomial distribution, since probability of renting remains constant at 70% throughout, and assuming independence of rentals. Also the number of trials (150) is known.
Parameters of the distribution are:
n=150, p=0.7
we look for
 for x=110 to 150
The summation may be carried out to get
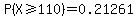
In practice, it is usual to use the normal approximation with continuity correction:
P(X>=110) is approximated by calculating the equivalent normal parameters,
mean = np=105
variance = npq=31.5
standard deviation = sqrt(npq)=5.6125
Therefore, using normal approximation,
Answer:
Using binomial distribution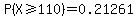
using normal approximation, with continuity correction,
 (approx.)
|
|
|
