SOLUTION: One number is 5 more than another. The difference between their squares is 105. What are the numbers?

Let x be the greater number, and let y be the smaller one.

Then we have two equations from the condition

x - y = 5,           (1)

and

 = .     (2)

Factor (2):

(x-y)*(x+y) = 105.   (3)

Replace the first factor in (3) by 5, in accordance with (1). You will get

5*(x+y) = 105,   hence

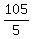x + y =  = 21.   (4)

Thus you have the system of two equations (1) and (4):

x - y = 5,   (1')   and
x + y = 21.  (4')

Add (1') and (4'). You will get 2x = 26. Hence, x = 13.

Distract (1') from ((4'). You will get 2y = 16. Hence, y = 8.

Answer. x = 13, y = 8.