Question 1010828: At the beginning of each year Bill Ross invest $1,400 semiannually at 8% for nine years. determine the cash value of this annuity do at the end of the ninth year ?
A. 37,339.68 B. 37,399.68 C. 37,939.86 D. 38,739.68
9*2=18
8% / 2= 4%
Factor = 12.4876
1400 * 12.4876= 17482.62
Which is not an option
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! it appears that this is an annuity where the payment is at the beginning of each time period.
i got 37,339.72 which looks very close to 37,339.68 shown in selection A.
not sure where you got your factor from, but it doesn't appear to be correct.
it should have come from the future value of an annuity table, or through the use of a time value of money calculator, or through the use of a formula that was manually derived.
i used the financial calculator shown in this link.
http://arachnoid.com/finance/index.html
the results of my analysis are shown here:

the factor that you would use in a future value of an annuity factor table is shown here.
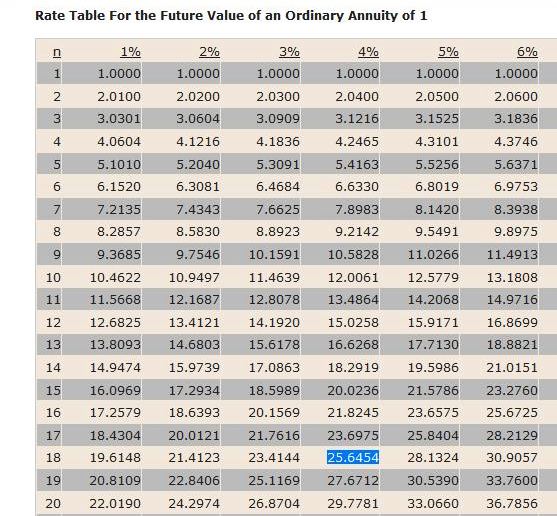
since the factor table assumes end of period payments, and you are dealing with beginning of period payments, you would multiply the factor shown by 1.04 before applying it.
if you do so, it should give you the same answer the calculator gave your, or something very close to it.
the factor table i used can be found at the following link:
http://www.accountingtools.com/future-value-of-ordinary-annui
you would use the following formula if you were to calculate it manually.
f = pmt * ((1+r)^n - 1) / r * (1+r)
pmt = 1400
r = .04
n = 18
formula becomes:
f = 1400 * (1.04^18 - 1) / .04 * 1.04
solve for f to get f = 37,339.72
i'm not sure where they got the 37,339.68 from but i suspect the difference is due to rounding of some intermediate result somewhere.
i would definitely go with selection A.
|
|
|