SOLUTION: If the 4th term of an arithmetic series is 62 and the 14th term is 122. Determine the sum of the first 30 terms.

From the condition, we have two equations for 4-th and 14-terms of the AM:

  =  62   and
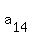 = 122.

Or

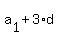  =  62,   (1)
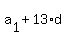 = 122.   (2)

Distract the equation (1) from the equation (2). You will get

10*d = 122 - 62 = 60.

Hence, d = 6. Thus the common difference of the given AM is 6.

Having this, you can easily find the first term of the AM from (1). It is

 = 62 - 3*6 = 44.

Now, when you know everything about the given AM, you can easily calculate the sum of the first n terms. 
Use the formula for the sum of the first n terms of arithmetic progression
(see the lesson Arithmetic progressions in this site). The sum is 

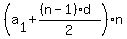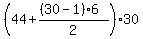 =  =  = 3930.