Question 1010767: Frank noticed that right now his dad, Peter, is five times older than his age. Last year, Frank's age was half that of his brother, John. Nine years from now, Peter will be twice as old as John. What is the sum of the current ages of Frank, John, and Peter?
So far, I figured that
Peter = 5(frank)
Frank = 1/2(john)+1
John = 2(peter)-9
Found 2 solutions by MathLover1, MathTherapy:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Frank noticed that right now his dad, Peter, is five times older than his age.
 .....eq.1 .....eq.1
Last year (means current age minus  ), Frank's age was half that of his brother, John. ), Frank's age was half that of his brother, John.

=>
=>
=> ..........eq.2 ..........eq.2
Nine years from now (means current age plus  , Peter will be twice as old as John. , Peter will be twice as old as John.

=>
=>
=> .......eq.3 .......eq.3
What is the sum of the current ages of Frank, John, and Peter?
from eq.1 and eq.3 we have

 .....eq.4 .....eq.4
from eq.2 and eq.4 we have
 .....solve for .....solve for 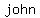
 .......cross multiply .......cross multiply




go to  .....eq.4, substitute .....eq.4, substitute  for for 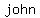
 .....eq.4 .....eq.4




go to  .......eq.3 , substitute .......eq.3 , substitute  for for 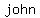


so, the sum of the current ages of Frank, John, and Peter is:

Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Frank noticed that right now his dad, Peter, is five times older than his age. Last year, Frank's age was half that of his brother, John. Nine years from now, Peter will be twice as old as John. What is the sum of the current ages of Frank, John, and Peter?
So far, I figured that
Peter = 5(frank)
Frank = 1/2(john)+1
John = 2(peter)-9
FYI: Five times older is worded incorrectly. It should be five times AS OLD
Let Frank’s be F
Then Peter’s (Dad’s) is: 5F
John’s age: 2F - 1
5F + 9 = 2(2F – 1 + 9)
5F + 9 = 2(2F + 8)
5F + 9 = 4F + 16
5F – 4F = 16 – 9
F, or Frank’s age is: 7
Peter’s: 5(7), or 35
John’s: 2(7) – 1, or 14 – 1, or 13
Sum of their ages: 7 + 35 + 13, or  years years
|
|
|