consider the following scalar equation of a plane. x+3y+z=0
Find the orthogonal complement of the vector <1,2,1>.
We want to find the set of vectors parallel to the plane that are
perpendicular to the vector <1,2,1>.
Vectors in or parallel to the plane are vectors < x,y,z > such that
x+2y+z = 0
Vectors perpendicular to <1,3,1> are < x,y,z > such that
<1,3,1>∙< x,y,z > = x+3y+z = 0
So we have this under-determined system
Subtracting them we get y = 0
Substituting we get x+2(0)+z = 0, or x+z=0, or z=-x
So the orthogonal complement is the set of vectors of the form
< k,0,-k >
Also find the point on the plane which is closest to (3,4,1).
That is the perpendicular distance from the point. We use the
formula for the perpendicular distance from the point
(x1, y1, z1) to the plane
ax + by + cz + d = 0, which is:
is 
So in our case (x1, y1, z1) = (3,4,1),
a=1, b=3, c=1, d=0
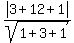
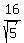Edwin
