|
Question 1010751: If f(x) is an odd function with a negative leading coefficient, g(x) is an even function with a negative leading coefficient, and h(x) is the product of f(x) and g(x), which of the following could be the graph of h(x)?
It;s not A).
link of graph ; http://prntscr.com/9f1q3t
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the term with the largest exponent determines the end behavior of the graph of the equation.
if x^3 is the largest exponent in the equation, the equation will become negative as x becomes more negative, and the equation will become positive as x becomes more positive, as shown below.
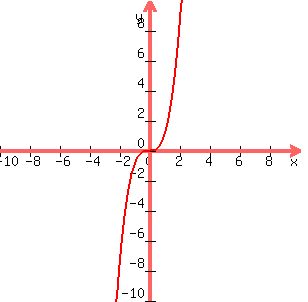
if the coefficient is negative, the behavior will reverse.
in that case, the equation will be positive on the left and negative on the right, as shown below.
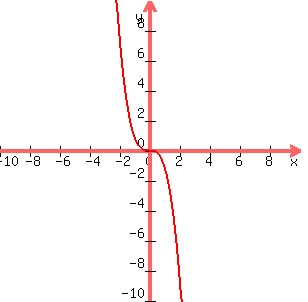
if x^4 is the largest exponent in the equation, the equation will become positive as x becomes more negative, and the equation will become positive as x becomes more positive, as shown below.
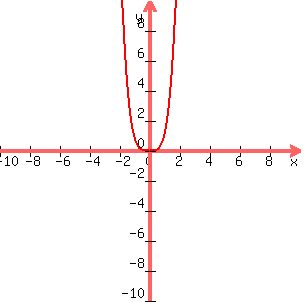
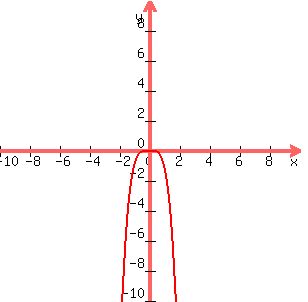
if the coefficient is negative, the behavior will reverse.
in that case, the equation will be negative on the left and negative on the right, as shown below.
if you have an odd function, you will have odd exponents (1,3,5,etc).
if you have an even function, you will have even exponents (2,4,6,etc).
if you multiply an equation with an odd exponent in the leading term and an even exponent in the leading term, will be odd because the exponents are additive.
x^3 * x^4 = x^(3+4) = x^7.
3 is odd, 4 is even, 7 is odd.
if the coefficients of both those terms are negative, the product will be positive.
(-x^3) * (-x^4) = -1 * x^3 * -1 * x^4 = 1 * x^7
you will have a leading term with an odd exponent and the coefficient will be positive.
the resulting equation will be negative on the left and positive on the right, as shown below.
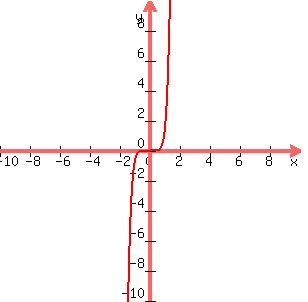
the terms with eponents less than the leading term are irrelevant. their impact will determine when the ends of the equation reach their potential, but they can't change it because as x gets larger and larger, the leading term will eventually dominate and determine the end direction.
to prove that, here are two equations with negative coefficients.
the first is an odd function and the second is an even function.
-x^3 + x is an odd function because f(-x) = x^3 - x which is the reverse of f(x). the graph of this function will be symmetric about the origin, as shown below:

-x^4 + x^2 is an even function because f(-x) = -x^4 + x^2 which is the same as f(x). the graph of this function will be symmetric about the y-axis, as shown below:

when you multiply these functions together, you get:
(-x^3 + x) * (-x^4 + x^2) = x^7 - 2x^5 + x^3
this has a leading term of x^7.
the exponent of the leading term is negative.
the coefficient of the leading term is positive because a negative * a negative yields a positive.
the graph of the equation will be negative on the left and positive on the right, as shown below:

what happens in between the two ends of the grpah is not so easy to determine.
the behavior at the ends, however, can easily be determined by analyzing the behavior of the leading term.
looking at your possible selections, the only one that starts negative and ends positive is selection A.
all you need to do is graph an even function times an odd function and the graph will show you.
i did just that in my last graph.
here's a good online graph software that you can use.
https://www.desmos.com/calculator
not sure why you said it's not selection A.
it sure looks like selection A to me.
this was confirmed by logic and by graphing.
|
|
|
| |