Question 1010718: identify the conic section if it is a parabola give the vertex if it is a circle give the center and radius if it is a ellipse or a hyperbola give the center and foci
5x^2-5y^2+40x-20y+35=0
Found 2 solutions by MathLover1, MathTherapy:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 .........all terms divide by .........all terms divide by 

 ...complete squares ...complete squares





 => both sides divide by => both sides divide by 
 => so, we have a hyperbola with => so, we have a hyperbola with  , ,
the center is at ( , , ) )
semimajor axis length | ~~ ~~
semiminor axis length |  ~~ ~~
foci is fixed distance  from the center from the center
 => => => =>

so, foci is at:
(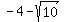 , , ) and ( ) and (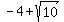 , , )~~( )~~(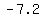 , ,  ) and ( ) and (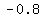 , ,  ) )
vertices | (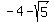 , , ) and ( ) and (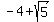 , ,  )~~( )~~(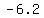 , ,  ) and ( ) and (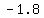 , ,  ) )
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
identify the conic section if it is a parabola give the vertex if it is a circle give the center and radius if it is a ellipse or a hyperbola give the center and foci
5x^2-5y^2+40x-20y+35=0
This is INDEED a HYPERBOLA, since higher-degree x and y have different signs.
However, that person is WRONG, as usual, because the equation you're looking for is: 
|
|
|