Question 1010315: find all other zeros give 2i is one zero.
f(x) = x^5 - 3x^4 + 5x^3 - 15x^2 + 4x - 12
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39625)   (Show Source):
You can put this solution on YOUR website! The TWO imaginary zeros are 2i and -2i, giving the quadratic factor  .
Use polynomial division to obtain the degree three factor of the function, and use whatever you know to further factorize it, such as try Rational Roots Theorem and synthetic division to check possible roots.
The result from the polynomial division (process not shown here) is
 .
You now want to look for up to three possible real, rational roots among the possibilities of -1, -3, 1, 3. The only one of those that worked was....
3, for the linear binomial factor  and quotient  .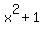
The listing of these three other roots then is:
3, i, -i.
Answer by MathTherapy(10555)  (Show Source):
|
|
|
