SOLUTION: I was doing some practice problems when I came across a very difficult question. Here is my problem. Please help. A real estate investor is examining a triangular plot of land.

Algebra ->  Matrices-and-determiminant -> SOLUTION: I was doing some practice problems when I came across a very difficult question. Here is my problem. Please help. A real estate investor is examining a triangular plot of land.       Log On


   

Question 1009952: I was doing some practice problems when I came across a very difficult question. Here is my problem. Please help.
A real estate investor is examining a triangular plot of land. She measures each angle of the field. The sum of the first and second angles is 78° more than the measure of the third angle. If the measure of the third angle is subtracted from the measure of the second angle, the result is twice the measure of the first angle. Find the measure of the sum of the first and second angles.
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39630) About Me  (Show Source):
You can put this solution on YOUR website!
You can take the description, assign variables, and form two equations. Are you then forgetting that ONE MORE EQUATION is the sum of the angles being 180 degrees? Is this enough for you to continue and finish?

Let measures of angles 1, 2, 3, be x, y, z.
The description first gives you system%28x%2By=78%2Bz%2Cy-z=2x%29.

When simplifying and using the 180 degree sum,
the system to solve will be system%28x%2By-z=78%2C2x-y%2Bz=0%2Cx%2By%2Bz=180%29.
The rest is yours to do. You will maybe use Cramer's Rule or some other linear algebra row-reduction, or something.


RESULTS:
x=126,y=53,z=1

Answer by MathTherapy(10557) About Me  (Show Source):
You can put this solution on YOUR website!
I was doing some practice problems when I came across a very difficult question. Here is my problem. Please help.
A real estate investor is examining a triangular plot of land. She measures each angle of the field. The sum of the first and second angles is 78° more than the measure of the third angle. If the measure of the third angle is subtracted from the measure of the second angle, the result is twice the measure of the first angle. Find the measure of the sum of the first and second angles.
Let measure of 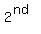1%5E%28st%29 and 2%5E%28nd%29 angles be F, and S, respectively

Then measure of 3rd angle is: F + S - 78

Also, S - (F + S – 78) = 2F______S – F – S + 78 = 2F______- F + 78 = 2F_____3F = 78

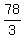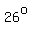
F, or 1%5E%28st%29 angle measures: 78%2F3, or 26%5Eo

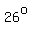
Measure of 1%5E%28st%29 angle: 26%5Eo

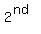Measure of 2%5E%28nd%29 angle: S

Measure of 3%5E%28rd%29 angle: F + S – 78, or 26 + S - 78, or S - 52

We then get: 26 + S + S – 52 = 180 ------ Angles of a triangle are supplementary

2S – 26 = 180

2S = 180 + 26

2S = 206

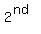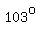
S, or 2%5E%28nd%29 angle measures: 206%2F2, or 103%5Eo



Sum of the measures of the 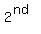1%5E%28st%29 and 2%5E%28nd%29 angles: 26 + 103, or highlight_green%28129%5Eo%29