SOLUTION: If 3cosx-4sinx=5,then 3sinx+4cosx=?

Algebra ->  Trigonometry-basics -> SOLUTION: If 3cosx-4sinx=5,then 3sinx+4cosx=?      Log On


   

Question 1009849: If 3cosx-4sinx=5,then 3sinx+4cosx=?
Answer by ikleyn(52847) About Me  (Show Source):
You can put this solution on YOUR website!
.
If 3cosx - 4sinx = 5, then 3sinx + 4cosx =?
----------------------------------------- 
3*cosx - 4*sinx = 5.            (1)

Let us rewrite this equation in the form

3%2F5.cos(x) - 4%2F5.sin(x) = 1.     (2)

Now consider the right-angled triangle with the sides (3,4,5), and let alpha be its smallest of two acute angles.

Then sin%28alpha%29 = 3%2F5 and cos%28alpha%29 = 4%2F5,

so we can rewrite the left side of the equation (2) in the form 

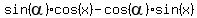sin%28alpha%29%2Acos%28x%29+-+cos%28alpha%29%2Asin%28x%29 = 1,   or

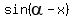sin%28alpha+-+x%29 = 1.

It implies that 

alpha+-+x = pi%2F2   and

cos%28alpha+-+x%29 = 0.                  (3)

But, from the other side, 

cos%28alpha-x%29 = cos%28alpha%29%2Acos%28x%29 + sin%28alpha%29%2Asin%28x%29.

Now substitute here cos%28alpha%29 = 4%2F5 and sin%28alpha%29 = 3%2F5, and you will get

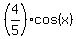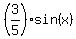%284%2F5%29%2Acos%28x%29 + %283%2F5%29%2Asin%28x%29 = 0.   (4)

As a last step, multiply both sides of (4) by 5, and you will get

4*cos(x) + 3*sin(x) = 0.

The problem is solved.

Answer.  If 3cosx - 4sinx = 5, then 3sinx + 4cosx = 0.