SOL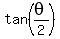UTION: Use a Double- or Half-Angle Formula to solve the equation in the interval [0, 2π). (Enter your answers as a comma-separated list.) tan(θ/2) − sin(θ) = 0

Algebra ->  Trigonometry-basics -> SOLUTION: Use a Double- or Half-Angle Formula to solve the equation in the interval [0, 2π). (Enter your answers as a comma-separated list.) tan(θ/2) − sin(θ) = 0      Log On


   

Question 1009490: Use a Double- or Half-Angle Formula to solve the equation in the interval [0, 2π). (Enter your answers as a comma-separated list.)
tan(θ/2) − sin(θ) = 0
Answer by ikleyn(52817) About Me  (Show Source):
You can put this solution on YOUR website!
.
Solve tan%28theta%2F2%29 - sin%28theta%29 = 0.
------------------------------------------------ 
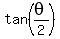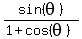The half-argument formula says that tan%28theta%2F2%29 = sin%28theta%29%2F%281%2Bcos%28theta%29%29. 

(See, for example, the lesson Trigonometric functions of half argument in this site).


Substitute it into the original equation, and you will get

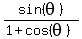sin%28theta%29%2F%281%2Bcos%28theta%29%29 - sin%28theta%29 = 0.

Now factor it:

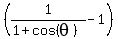sin%28theta%29.%281%2F%281%2Bcos%28theta%29%29-1%29 = 0.

Thus you get two equations:

1) sin%28theta%29 = 0,  which has two solutions  theta = 0 and pi in the given interval for theta.


2) 1%2F%281%2Bcos%28theta%29%29-1 = 0,  or  cos%28theta%29 = 0,  which has two solutions  theta = pi%2F2 and 3pi%2F2 in the given interval for theta.

Answer. The solutions are theta = 0, pi%2F2, pi and 3pi%2F2.