Question 1009151: Find the points of intersection, if any, of the pair of curves :
x^2+y^2=13 , y=x+1
Answer by ikleyn(52794)   (Show Source):
You can put this solution on YOUR website! .
Find the points of intersection, if any, of the pair of curves :
x^2+y^2=13 , y=x+1
----------------------------------------------------------------
Substitute y from the second equation into the first one. In this way you exclude y and obtain single equation for variable x:
 +  =  .
Simplify and solve this quadratic equation:
 =  ,
 = .
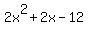The roots are  = -3 and  = 2.
Hence, the pairs (x,y) = (-3,-2) and (2,3) are our intersection points.
Answer. the pairs (x,y) = (-3,-2) and (2,3) are the two intersection points.
|
|
|
