SOLUTION: given y=2x^2+bx+c, the minimum value is -3 and the graph intersects at (0,-1). Find the values of b and c.

Instead of doing your problem for you, I'll do one exactly in every
detail step-by-step like yours.  All you have to do is use it as a
model and do the exact same steps.  So instead of your problem
I will do this one with only the numbers changed. I didn't even
change the 2 coefficient of x^2.

given , the minimum value is -11 and the graph 
intersects at (0,-3). Find the values of b and c.

Since the equation passes through (0,-3) we substitute
(x,y) = (0,-3) into the given equation:

-3=2(0)²+b(0)+c
-3=0+0+c
-3=c

Therefore we already have the value of c, and

 becomes:



The minimum value of a quadratic equation is the y-coordinate
of the vertex. The formula for the x-coordinate of the vertex is



Since a=2 this becomes 

Thus when we substitute the x coordinate of the vertex ,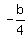
we will get the y coordinate of the vertex which will be the
maximum value of -11.  So we substitute 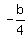 for x and -11
for y in


 


Add 3 to both sides:







Multiply through by 8









Thus there are two solutions for b, and 1 solution for c

Checking, we draw the graphs of

  and  



Edwin