Question 1008642: Given the quadratic function y=ax^2+bx+c, the maximum value is a^2+4 at x=1 and the graph passes through the point (3,1). Find the values for a, b and c.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given the quadratic function y=ax^2+bx+c, the maximum value is a^2+4 at x=1 and the graph passes through the point (3,1).
Find the values for a, b and c.
:
At x^2 + 4, when x=1, find y
y = 2^2 + 4
y = 5
:
We know the axis of symmetry (max value) x=1
The given point to the right is 3,1
Therefore the point to left is -1,1
:
Three equations we can use to find a, b, c
:
-1, 1: a - b + c = 1
1, 5: a + b + c = 5
3, 1: 9a + 3b + c = 1
:
We can use the 1st two equations to find b
a + b + c = 5
a - b + c = 1
-----------------Subtraction eliminates a and c
2b = 4
b = 2
:
using 2nd and 3rd equations, replace b with 2
9a + 3(2) + c = 1
9a + 6 + c = 1
9a + c = -5 (subtracted 6 from both sides)
and
a + 2 + c = 5
a + c = 3
Use elimination with theses two equations to find a
9a + c = -5
a + c = 3
--------------Subtraction eliminates c, find a
8a = -8
a = -1
:
Use the 2nd original equation, a + b + c = 5; to find c, replace a and b
-1 + 2 + c = 5
c = 5 - 1
c = 4
:
Our equation: y = -x^2 + 2x + 4, (green)
:
Plotting the given equation and the above equation
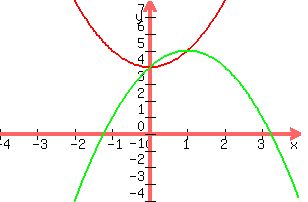
You can see the max occurs where the two curves intersect; x=1; y=5
|
|
|