Question 1008465: One positive number is three more than twice a number that the product equals 1430.what are the numbers?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE UNEXPECTED WAY TO SOLVE IT:
The prime factorization of 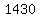 is is
 . .
Because there are  prime factors, each with an exponent of prime factors, each with an exponent of  , ,
the number of possible factors of 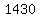 is is
 . .
That makes  factor pairs: factor pairs:
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 , and , and
 . .
The first six pairs have factors that are too far apart to be solutions.
 so so  and and 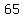 are not the two factors. are not the two factors.
 , so , so  are the two numbers. are the two numbers.
THE EXPECTED WAY TO SOLVE IT:
 = the smallest positive number mentioned first = the smallest positive number mentioned first
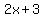 = the second number = three more than twice the first number = the second number = three more than twice the first number
 = the product of the two numbers = the product of the two numbers
 <--> <--> <--> <-->
You can solve the quadratic equation above by the method of your choice
("completing the square", factoring, or using the quadratic formula),
and you get the solutions  . .
Factoring:
 --> --> --> --> --> --> --> --> --> -->
Since the first number mentioned was a positive number,
the solution is  ---> ---> ---> --->
Using the quadratic formula,
which says that the solutions to 
are given by  : :
In this case  , ,  , ans , ans  , so , so



 ---> --->
Completing the square:







 --> --> --> --> --> -->
|
|
|