|
Question 1008452: Please how to solve this, using math rules?.
show solution please!
9-3÷4x5+10=?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! We could have more intuitive "math rules" where we would write
 as as  , ,
but we would use lots of parentheses.
To use less parentheses, we have the math rules that everyone has to agree to .
Those rules say that:
1) (P or B) parentheses (also called brackets) rule;
2) we give multiplication/division (MD) priority over addition/subtraction (AS), and
3) otherwise we work step by step from left to right.
In the US, teachers may try to help you remember the rules by using the abbreviation
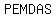 or or   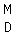 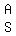 in the US, in the US,
for "Please Excuse My Dear Aunt Sally".
(The  is for Exponents, that were not involved in your calculation). is for Exponents, that were not involved in your calculation).
In the UK, they use 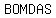 or or   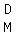 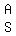 . .
So,
 
The result can also be written as a mixed number:

EXPLANATION:
The "math rules" are conventions adopted to make communication easier.
Suppose you buy 2 T-shirts at $5 each, 4 shorts at $12 each, and 3 hats at $5 each.
In fourth grade you would perform one operation at a time,
just like a baby at first speaks in isolated words.
You would calculate the total in several steps:
what you paid for the T=shirts as  , ,
what you paid for the T=shirts as  , ,
what you paid for the T=shirts as  , ,
and then you would add the results of the previous calculations.
People eventually get to communicate in long sentences,
using the conventions (grammar rules) of their audience so that the meaning is properly understood.
The calculation of the total above could be described in one line as
 , ,
and you would probably understand that you have to do the calculations described above, in the order described.
A longer string of calculations like that is done very often,
and it would take a lot of parentheses to write it.
Because of that, many, many years ago, people agreed that multiplications are done first,
and now we write that as  , ,
expecting that you will calculate it (as usual) as

The same goes for divisions as for multiplications,
because divisions are really multiplications:
dividing by  is really multiplying times is really multiplying times  , ,
dividing by  is really multiplying times is really multiplying times  , and so on. , and so on.
Once you accept fractions (rational numbers),
division can be seen as a reflection of multiplication;
it may look real just as an image in a mirror, but it is just multiplication.
While I am at it, can I tell you that subtraction is not real either.
After all, subtracting  is really adding the negative number is really adding the negative number  . .
|
|
|
| |