|
Question 1008375: If 5 men and 3 boys can reap 23 acres in 4 days and 3 men and 2 boys can reap 7 acres in 2 days , how many boys must assist 7 men in order that they may reap 45 acres in 6 days?
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If 5 men and 3 boys can reap 23 acres in 4 days and 3 men and 2 boys can reap 7 acres in 2 days , how many boys must assist 7 men in order that they may reap 45 acres in 6 days?
-------------------------------------------------------------
Let m be (an unknown) rate of work for one man, measured in  ,
and let b be (an unknown) rate of work for one boy, measured in same units.
Then we have a system of two linear equations in two unknowns m and b
4*(5m + 3b) = 23, (1)
2*(3m + 2b) = 7. (2)
Or
20m + 12b = 23, (1')
6m + 4b = 7. (2')
To solve it, multiply (2') by 3 and then distract it from (1'). You will get
20m - 18m = 23 - 3*7, or
2m = 2, hence, m = 1.
Substitute it into (2'), and you will get 4b = 7 - 6 = 1, hence, b = ,
and let b be (an unknown) rate of work for one boy, measured in same units.
Then we have a system of two linear equations in two unknowns m and b
4*(5m + 3b) = 23, (1)
2*(3m + 2b) = 7. (2)
Or
20m + 12b = 23, (1')
6m + 4b = 7. (2')
To solve it, multiply (2') by 3 and then distract it from (1'). You will get
20m - 18m = 23 - 3*7, or
2m = 2, hence, m = 1.
Substitute it into (2'), and you will get 4b = 7 - 6 = 1, hence, b =  .
Thus you obtained that 1 man can reap 1 acr in 1 day, while 1 boy can reap .
Thus you obtained that 1 man can reap 1 acr in 1 day, while 1 boy can reap  of acr in 1 day.
Then 7 men in 6 days can reap 7*6*1 = 42 acres.
How many boys must assist to reap remaining 45-42 = 3 acres acres in 6 days?
Their number is of acr in 1 day.
Then 7 men in 6 days can reap 7*6*1 = 42 acres.
How many boys must assist to reap remaining 45-42 = 3 acres acres in 6 days?
Their number is 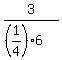 = =  = 2.
Answer. Two boys. = 2.
Answer. Two boys.
|
|
|
| |