SOLUTION: find the largest angle in a triangle Side A is (x+2)degrees angle B is (2x)degrees Angle C is (7x+10)degrees

Algebra ->  Triangles -> SOLUTION: find the largest angle in a triangle Side A is (x+2)degrees angle B is (2x)degrees Angle C is (7x+10)degrees      Log On


   

Question 1008230: find the largest angle in a triangle Side A is (x+2)degrees angle B is (2x)degrees Angle C is (7x+10)degrees
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Angle A measures (x+2)degrees, angle B measures (2x)degrees, and Angle C measures (7x+10) degrees.
We all know that the measures of the angles of a triangle add up to 180 degrees, so
%28x%2B2%29%2B%282x%29%2B%287x%2B10%29=180 degrees.
All we have to do is solve for x, calculate the measures of the angles, and find the largest one.
%28x%2B2%29%2B%282x%29%2B%287x%2B10%29=180
x%2B2%2B2x%2B7x%2B10=180
%28x%2B2x%2B7x%29%2B%282%2B10%29=180
10x%2B12=180
10x=180-12
10x=168
x=168%2F10
x=16.8
So, angle C measures
(7x+10) degrees =7%2816.8%29%2B10degrees =117.6%2B10degrees =highlight%28127.6%29 degrees.
Since C so large that its measure, 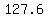127.6 ,
is larger than half of the sums of the measures, 180%2F2=90 ,
C must be the largest angle.