Question 100726: Translate the following statement into an inequality. Let x represent the number.
The cost for a long-distance telephone call is $0.36 for the first minute and $0.21 for each additional minute or portion thereof. Write an inequality representing the number of minutes a person could talk without exceeding $3.
Found 2 solutions by checkley71, oberobic:
Answer by checkley71(8403)   (Show Source):
Answer by oberobic(2304) (Show Source):
You can put this solution on YOUR website! Let x represent 1 less than the total number of minutes for a long-distance phone call. The total cost of the call is 36 cents ($0.36) for the first minute plus 21 cents ($0.21) for each additional minute. So, the number of minutes that cost .36 is 1, by definition. And the total minutes at .21 = x. (Remember, x is one less than the total number of minutes: you're charged .36 for the first minute, so you don't want to pay for it twice by including it in x.)
Given you want the call to cost less than $3, the inequality is:
 .
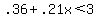Solving the inequality is needed to check the solution. Begin with the equivalent equation:
Multiply through by 100 to remove the decimals, which makes the work easier.
Subtracting 36 from both sides, we have:
Dividing both sides by 21, we have:
 .
Returning to the inequality, when 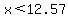 , the total cost of the long-distance call will be less than $3.
Check by substituting.
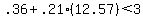 , which equals 2.9997. Check.
Keep in mind that if asked how long you could talk, you would have to add back the first minute. So x+1 = 13.57, which is how long the phone call could be and still cost less than $3.
|
|
|
