SOLUTION: Show that P(1,2), Q(-11,2) and R(-5,6) are vertices of an isosceles triangle. Find the Lengths of all three sides PQ= QR= PR= Please help I have no Idea where to start...

Algebra ->  Triangles -> SOLUTION: Show that P(1,2), Q(-11,2) and R(-5,6) are vertices of an isosceles triangle. Find the Lengths of all three sides PQ= QR= PR= Please help I have no Idea where to start...      Log On


   

Question 1006809: Show that P(1,2), Q(-11,2) and R(-5,6) are vertices of an isosceles triangle.
Find the Lengths of all three sides
PQ=
QR=
PR=
Please help I have no Idea where to start...
Found 3 solutions by josgarithmetic, jim_thompson5910, MathTherapy:
Answer by josgarithmetic(39621) About Me  (Show Source):
You can put this solution on YOUR website!
Courses and books for Geometry and for Intermediate Algebra present and discuss the Distance Formula, which is a slight rearrangement of the Pythagorean Theorem right triangle sides relationship.

The distance between two points (r,p) and (v,w) in two dimensions is 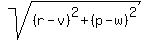sqrt%28%28r-v%29%5E2%2B%28p-w%29%5E2%29.

Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Use the distance formula to calculate the distance between each pair of points.

Example: the distance between P and Q is equal to the length of side PQ.

The distance formula is d+=+sqrt%28%28x%5B1%5D-x%5B2%5D%29%5E2%2B%28y%5B1%5D-y%5B2%5D%29%5E2%29

You can use this solver
http://www.algebra.com/algebra/homework/Length-and-distance/distance-formula.solver
to calculate the three distances to get the side lengths


Using the solver, the segment lengths are

PQ=12
QR=2%2Asqrt%2813%29
PR=2%2Asqrt%2813%29

So we see that QR+=+PR. We have exactly 2 equal sides. So this triangle is definitely an isosceles triangle.

Answer by MathTherapy(10555) About Me  (Show Source):
You can put this solution on YOUR website!

Show that P(1,2), Q(-11,2) and R(-5,6) are vertices of an isosceles triangle.
Find the Lengths of all three sides
PQ=
QR=
PR=
Please help I have no Idea where to start...
Since P & Q have the same y-coordinate, PQ is a HORIZONTAL LINE that's parallel to the x-axis. Its distance is therefore 1 - - 11, or 12. 

Now just use the distance (d) formula: d+=+sqrt%28%28x%5B1%5D+-+x%5B2%5D%29%5E2+%2B+%28y%5B1%5D+-+y%5B2%5D%29%5E2%29 to find the distances from P(1, 2) to R(- 5, 6) and from Q(- 11, 2) to R(- 5, 6).

These 3 distances should reveal whether ΔPQR is isosceles or not.