SOLUTION: The number 2015 can be written as the sum of two or more consecutive positive integers in seven different ways. Find the total of the smallest integers from each of the seven wa

Let x represent the smallest integer in any case of consecutive
integers with sum 2015.

The sum of n consecutive positive integers beginning with x, 
using the sum formula for an arithmetic sequence 



with a1=x and d=1



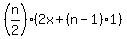Setting that equal to 2015



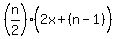
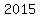Multiplying both sides by 2 to clear the fraction
and simplifying:









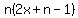
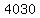
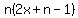
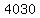
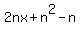
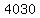
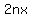
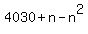
, the smallest integer.

From ,

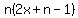
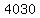we see that n, the number of terms, and 2x+n-1 make up a factor 
pair of 4030.  

We can factor 4030 into a pair of factors the following 8 ways:


n×(2x+n-1) = 4030, x = (4030+n-n^2)/(2n) = smallest integer
----------------------------------------
1×4030             x = 2015  <--ignore since only 1 integer, we need 2 or more  
2×2015             x = 1007                 
5×806              x =  401
10×403             x =  197
13×310             x =  149
26×155             x =   65
31×130             x =   50  
62×65              x =    2
---------------------------
               total = 1871  



The total of the smallest integers x is 1871

Answer: 1841

Edwin