SOLUTION: You hit a golfball vertically upward with your pitching wedge. The position function of the ball is s(t)= -3t^2 + 30t where the origin is at ground level and the positive direction

Algebra ->  Test -> SOLUTION: You hit a golfball vertically upward with your pitching wedge. The position function of the ball is s(t)= -3t^2 + 30t where the origin is at ground level and the positive direction      Log On


   

Question 1006616: You hit a golfball vertically upward with your pitching wedge. The position function of the ball is s(t)= -3t^2 + 30t where the origin is at ground level and the positive direction is vertically up. (distance in meters)
a) Find the maximum height reached by the ball.
b) Find the velocity of the ball as it reaches the ground.
c) Find the acceleration of the ball.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!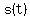
s%28t%29= height of the ball, in specified units of length.
What t means is not specified, so we assume
t= time elapsed since the ball was hit, in specified units of time.

a)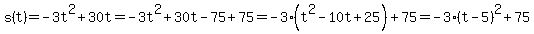
tells us that the maximum height reached by the ball is highlight%2875%29 unspecified units, which happens when t=5 .
You could also use memorized algebra "formulas", or calculus to find that with just as much effort.

b) If you are in calculus class, you would calculate that slope as
the value of the derivative ds%2Fdt=-6t%2B30 at t=0 ,
-6%2A0%2B30=30 .
If you are not in calculus class you would look for the slope of the tangent to the parabola at the point with t=0 and s=0 .
The graph of the quadratic function,
such as s%28t%29=-3t%5E2%2B30t ,
is a parabola with a vertical axis of symmetry:
graph%28300%2C300%2C-1%2C11%2C-20%2C80%2C-3x%5E2%2B30x%29 .
Because of its symmetry,
the slopes at the two points where s%28t%29=0 , t=0 and t=10
are opposite numbers (same absolute value, but positive at t=0 , negative at t=10 .
A line passing through that point has the equation s=mt ,
and would be tangent if it intersect the parabola at only one point,
meaning that the equation mt=-3t%5E2%2B30t<-->3t%5E2-30t%2Bmt=0<-->t%283t-30-m%29%29=0
has only one solution.
The solutions to that equation are t=0 and t=30-m .
If both solutions must be the same, then 30-m=0--->m=30 .
Any way you calculate it, the slope of the graph (speed of the ball) is
30 as he ball leaves the ground (positive meaning going up),
and highlight%28-30%29 as it hits the ground (negative meaning coming down).
What are the units? The speed is measured in unspecified unit of length per unspecified unit of time.

c) The acceleration of a ball moving with a linear trajectory described by
s%28t%29=-3t%5E2%2B30t is the second derivative
d%5E2s%2Fdt%5E2=highlight%28-6%29 , with unspecified units.
If you are hitting that ball on Earth, the negative value of the downwards acceleration due to gravity would be
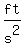-g=-9.8m%2Fs%5E2 or -g=-32ft%2Fs%5E2 ,
unless there is another unexplained, unexpected force acting on the ball.

NOTES:
Very strange problem. Looks as a calculus problem designed by a teacher who either
lives on a different planet, or
uses creative units of measurement, or
did not learn physics.
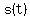s%28t%29 represents the height of the ball, but the units are not specified.
What t means is not specified,
but it must represent time since the ball was hit, in some equally unspecified units.
If that happens on planet Earth,
with time measured in seconds, and height in meters,
the coefficient of t%5E2 would be -4.9 .
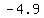If that happens on planet Earth,
with time measured in seconds, and height in feet,
the coefficient of t%5E2 would be -16 .
Everyone who studied physics should know that.