.
What would be the solutions to (sin2x + cos2x)^2 = 1?
-----------------------------------------------------
Start with
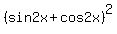 =
= 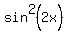 +
+  +
+ 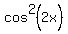 = 1 + 2*sin(2x)*cos(2x).
Therefore, your equation takes the form
1 + 2*sin(2x)*cos(2x) = 1, or
2*sin(2x)*cos(2x) = 0. (1)
Now, do you know this formula sin(2alpha) = 2*sin(alpha)*cos(alpha) ?
(See the lesson Trigonometric functions of multiply argument in this site).
It reduces the equation (1) to
sin(4x) = 0.
The solution is x =
= 1 + 2*sin(2x)*cos(2x).
Therefore, your equation takes the form
1 + 2*sin(2x)*cos(2x) = 1, or
2*sin(2x)*cos(2x) = 0. (1)
Now, do you know this formula sin(2alpha) = 2*sin(alpha)*cos(alpha) ?
(See the lesson Trigonometric functions of multiply argument in this site).
It reduces the equation (1) to
sin(4x) = 0.
The solution is x = 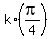 , k = 0, +/-1, +/-2, . . .
It is the solution of your original equation.
, k = 0, +/-1, +/-2, . . .
It is the solution of your original equation.