Question 1006529: (1+2+3+...+19)20
----------------------------- =
(21+22+23+...+39)40
Find 3 (n)s
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
What to find ?
-------------------------------------------------------------
Comment from student: simplify it into an expression using n
-------------------------------------------------------------
OK. (Why do not write it from the very beginning?)
The sum in the numerator is the sum of first 19 terms of an arithmetic progression 1, 2, 3, . . . , 19
S = 1 + 2 + 3 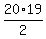+ . . . + 19 =  =  = 10*19.
The sum in the numerator is the sum of first 19 terms of an arithmetic progression 21, 22, 23, . . . , 39
T = 21 + 22 + 23 + . . . + 3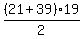9 =  =  = 30*19.
Hence, the ratio you are asking for, is
 =  =  =  .
|
|
|
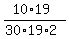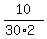