SOLUTION: -3cos(pi/2 - X) = tanX

cos(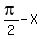) = sin(X), according to reduction formula.

Therefore, your equation takes the form

-3*sin(X) = tan(X).   

Rewrite it in the form 

-3*sin(X) = 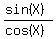, or, even better :)

-3*sin(X) = 

Now introduce the new variable u = sin(X) and square both sides of the last equation. You will get an equation for u:

 = .

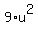Simplify it and solve step by step:

 =   ----->   =   ----->   =   ----->   = .

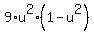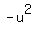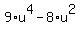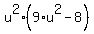The last equation comes apart in two equations. First one is 

 =   ----->  sin(X) = 0  ----->  X = 0, +- , +/- , . . . , +/- , . . . , k= 0, 1, 2, 3, . . . 

The second one is 

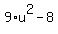 =   ----->   =   ----->   = +/-   ----->  sin(X) = +/- .  

It generates two families of potential roots: 

(a) X = +/- arcsin(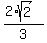) + , k = 0, +/-1, +/-2, +/-3, . . . and 

(b) X = +/- [] + , k = 0, +/-1, +/-2, +/-3, . . .

 
  

  
 

    


Figure. Plots -3*sin(x) (in red) and tan(x) (in green)

  
  
The roots (a) X = +/- arcsin(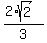) +  are excessive. They are not the solutions.

The roots (b) X = +/- [] +  are the solutions.