.
solve on the interval (0, 2pi)
cos(4X) - cos(6X) = 0
--------------------------------
Use the general formula for subtraction of cosines
 -
-  =
= 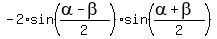 (see the lesson Addition and subtraction of trigonometric functions in this site).
In your case, it gives
(see the lesson Addition and subtraction of trigonometric functions in this site).
In your case, it gives
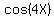 -
- 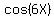 =
= 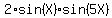 ,
and your equation takes the form
,
and your equation takes the form
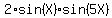 =
=  .
It comes apart in two equations. First one is
sin(X) = 0, and it produces the solutions X = +/-
.
It comes apart in two equations. First one is
sin(X) = 0, and it produces the solutions X = +/-  , k = 0, 1, 2, . . .
The second equations is sin(5x) = 0, and it produces the solutions X = +/-
, k = 0, 1, 2, . . .
The second equations is sin(5x) = 0, and it produces the solutions X = +/- 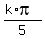 , k = 0, 1, 2, . . .
Of these two sequences, the second one overlays the first.
Taking into account the assigned interval, the solutions are
, k = 0, 1, 2, . . .
Of these two sequences, the second one overlays the first.
Taking into account the assigned interval, the solutions are 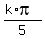 , k = 0, 1, 2, 3, . . . , 9.
, k = 0, 1, 2, 3, . . . , 9.