SOLUTION: Prove that the sum s of the first n natural numbers is given by the equation s = n/2 (n+1)

Algebra ->  Sequences-and-series -> SOLUTION: Prove that the sum s of the first n natural numbers is given by the equation s = n/2 (n+1)       Log On


   

Question 1006222: Prove that the sum s of the first n natural numbers is given by the
equation s = n/2 (n+1)

Answer by AnlytcPhil(1806) About Me  (Show Source):
You can put this solution on YOUR website!
First we show that the expression 

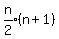expr%28n%2F2%29%28n%2B1%29

gives the sum of the first 2 natural numbers:

1+2 = 3

and the expression with n=2 substituted gives:

expr%282%2F2%29%282%2B1%29=%281%29%283%29+=+3

So the formula holds for n=k=22

Now we know that there is at least one natural number k=2 for which
the equation holds for n=k.

Next we show that under the assumption that we just showed, that 
there exists one natural number n=k for which the equation holds true, 
then the equation will also hold for n=k+1

Under the assumption that the expression gives the sum of the first
n=k natural numbers for some n=k, then

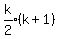expr%28k%2F2%29%28k%2B1%29

We add the next natural number (k+1) to the expression:

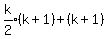expr%28k%2F2%29%28k%2B1%29%2B%28k%2B1%29

We factor out (k+1)



And this equals to the expression 

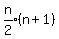expr%28n%2F2%29%28n%2B1%29 with k+1 substituted for n, since

expr%28%28k%2B1%29%2F2%29%28%28k%2B1%29%5E%22%22%2B1%29=expr%28%28k%2B1%29%2F2%29%28k%2B2%29

Now since we have shown that it is true when n=k=2, it is therefore
true when n=k+1=3.

Now since we have shown that it is true when n=k=3, it is therefore
true when n=k+1=4.

Etc., etc., 

Therefore there can be no first value of k for which the expression 
does not hold.  For if there were such first value, the expression
would hold for n=k-1 and therefore it would hold for n=k, which would 
be a contradiction to the assumption that there could be a natural 
number k for which the expression did not hold.

Edwin