I don't understand why the other tutor thought it mattered that
< -4,5 > was mentioned twice. Here is the picture of how it
is easily possible. I'll put all the vectors with their tails
at the origin:
 Your problem was:
Your problem was:
find two vectors v1 and v2 whose sum is <3,-2> where v1
is parallel to <-4,5> while v2 is perpendicular to <-4,5>.
As you can see from the graph, it certainly looks possible for v1
to be parallel to <-4,5> and v2 to be perpendicular to it.
And also the green lines show that the sum of v1 and v2 can
be <3,-2>.
[I hope it doesn't bother you that v1 and <-4,5> in the graph are
both on the same line and I said they are parallel. Remember that
vectors can be moved anywhere, and so vectors which are multiples
of each other are considered to be parallel because they can be
moved so that they are parallel by the usual standards of basic
geometry.]
So let's calculate what we see in the above drawing:
Since v1 is parallel to < -4,5 >, there is some non-zero scalar k
such that
v1 = < -4k,5k >
let v2 = < a,b >
Since v2 is perpendicular to < -4,5 > its dot product
with < -4,5 > is 0, so
v2•< -4,5 > = < a,b >•< -4,5 > = -4a+5b = 0
(1) -4a+5b = 0
Since v1 + v2 = <3,-2>
< -4k,5k > + < a,b > = < 3, -2 >
(2) -4k+a = 3
(3) 5k+b = -2
So we have this system of 3 equations in 3 unknowns:
 The variable "a" is already eliminated in the 3rd equation,
so we eliminate "a" from the 1st and 2nd equations, by
multiplying the 2nd equation by 4 and adding it to the
1st equation:
-4a + 5b = 0
4a + 16k = 12
-------------------
5b + 16k = 12
Now we have the system of 2 equations in 2 unknowns:
The variable "a" is already eliminated in the 3rd equation,
so we eliminate "a" from the 1st and 2nd equations, by
multiplying the 2nd equation by 4 and adding it to the
1st equation:
-4a + 5b = 0
4a + 16k = 12
-------------------
5b + 16k = 12
Now we have the system of 2 equations in 2 unknowns:
 Eliminate b by multiplying the second equation through
by -5 and adding it to the first equation:
5b - 16k = 12
-5b - 25k = 10
--------------
-41k = 22
k =
Eliminate b by multiplying the second equation through
by -5 and adding it to the first equation:
5b - 16k = 12
-5b - 25k = 10
--------------
-41k = 22
k = 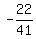 Substituting in
(2) -4k+a = 3
We get:
Substituting in
(2) -4k+a = 3
We get:




 Substituting in
(3) 5k+b = -2
We get:
Substituting in
(3) 5k+b = -2
We get:




 So the answer is:
v1 = < -4k,5k > =
So the answer is:
v1 = < -4k,5k > =  =
= 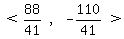 v2 = < a,b > =
v2 = < a,b > = 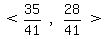 That's a pretty messy answer, but it's correct, and it looks
like it agrees with the drawing for v1 and v2 above.
Edwin
That's a pretty messy answer, but it's correct, and it looks
like it agrees with the drawing for v1 and v2 above.
Edwin