Question 1006063: The sides of a triangle are in the ratio 5:12:13 and its perimeter is 150 m. Find the area of triangle.
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52776)   (Show Source): (Show Source):
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The sides of a triangle are in the ratio 5:12:13 and its perimeter is 150 m. Find the area of triangle.
A triangle with sides 5, 12, and 13 represents a special right triangle. That's because 
To determine the length of each side, we let the multiplicative factor for the sides, be x
Therefore, the sides are: 5x, 12x, and 13x
With the perimeter being 150, we get: 5x + 12x + 13x = 150
30x = 150
x = 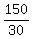 , or 5 , or 5
We now have the sides as:
5(5), or 25 m
12(5), or 60 m
13(5), or 65 m
Obviously, the 2 shorter sides are the legs, with either leg being the altitude
Area:  = = 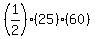 , or , or 
|
|
|