SOLUTION: It took an airplane 2 hours to fly 600 miles against a headwind. The return trip with the wind took 1 2/3 hours. Find the speed of the plane with no wind and the windspeed. (Assume

                rate          time         distance

AGAINST        r-w            2             600

WITH           r+w                     600

Let speed of plane in still air, and speed of wind speed, be S and W, respectively

Then total speed when going against the wind = S - W

Also, total speed when going with the wind = S + W

Therefore, we can say that: , or S – W = 300 ---- eq (i)

And, , or , or S + W = 360 ---------- eq (ii)

2S = 660 ------- Adding eqs (i) & (ii)

S, or speed in still air = , or  mph

330 – W = 300 -------- Substituting 330 for S in eq (i) 

- W = 300 – 330

- W = - 30

W, or wind speed = 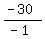, or  mph