Question 1005810: Help with special sequences?
I'm stuck on these two questions and it would be greatly appreciated if you could help me! Even if its one question, I would really like to get the whole concept to help prepare for my test! Thank you!!
1. Find the 4th term if the sequence in which a^1 = 2 and a^n+1 = -4a^n + 2.
2.Find the third iterate, x^3, of the function f(x) = 3x + 5 for an initial value of x^0 = 1.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! If  , the common ratio of consecutive terms is
 .
It is a geometric sequence, where each term is the one before multiplied by  ,
so as for all geometric sequences,  .
In particular,
 .
Since  and ,
 .
The 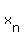 terms are iterations using 
Because the problem asked for the term  , with index  ,
it was easy enough to calculate each of the terms from the previous term until I got to .
No need to get more complicated.
If the problem had asked for a term with a much higher index, such as the 10th term,
I would have found a "formula" to get that term directly, without calculating all the terms in between.
Since 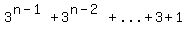 is the sum of a geometric sequence with first term  and common ratio  ,
that sum is  , so
That last "formula" applied to  , and with , yields
 .
|
|
|
