Question 1005593: Bacteria were introduced to a petri dish. Two hours after the introduction, there were 120411 bacteria. After seven hours since the introduction, there were 1083699 bacteria.
1.) Find the growth rate of the bacteria. (round to 3 decimal places)
2.) How many bacteria were initially introduced to the Petri dish? (Round to the nearest bacteria).
3.) How many bacteria will there be after 12 hours? (Round to the nearest bacteria).
4.) How long does it take for the bacteria colony to reach 361233 bacteria? (round to 2 decimal places)
Use Pe^rt equation!
PLEASE HELP ME !!!
Answer by josgarithmetic(39618)   (Show Source):
You can put this solution on YOUR website! This response is not a complete answer nor full solution...
There are two data points of (2, 120411) and (7, 1083699). The model you are using is  which is exponential. What you want is something LINEAR from this exponential equation, and some of your data, specifically the second coordinates, need to be modified. Use base for the Natural Logarithm, and find natural log of both sides of the equation. That will give you, upon appropriate simplification, the linear form of equation to use.
Your two data points would be (2, ln(120411) ) and (7, ln(1083699) ).
Much of the process is what you learned in "Algebra 1".
--
ADDITIONAL PROCESS DESCRIPTION
 -----Linear Form as Slope-Intercept form, slope is r, vertical axis intercept is  .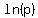
The points to use for help either in graphing or finding r, and p, are ( 2, 11.69867 ) and
(7, 13.85989).
You can use those two points, in that form, to find slope, and this slope will be the value for r.
Use the found slope and either of the treated points to calculate the vertical axis intercept, which will be the value of ln(p); and then use your calculator or log table to get the value of p.
Once those are found, you have a more specific model for .
|
|
|
