Question 1005463: Using the formula h=-1/2gt^2+v(0)t+h(0) (the zero in the parens is lower/small beneath the letter) and g= gravitational constant and v = upward velocity from a starting height of h.
1a. What is the height after three seconds of a penny dropped from the roof of the a tall building about 1250 feet tall?
1b. After how many seconds does the penny hit the ground?
2. What is the height after three seconds of a ball thrown from the roof of a building about 495 feet tall and is tossed upwards with a velocity of 10m/s?
2b. After how many seconds does it hit the ground?
Thanks in advance. I think I have the answers but want to check the work done.
Found 2 solutions by KMST, rothauserc:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  is a general formula. is a general formula.
For the first problem we will set:
 = time from the moment the penny is dropped (we will measure it in seconds, because it will be a short time), = time from the moment the penny is dropped (we will measure it in seconds, because it will be a short time),
 = height (in feet) at the moment, = height (in feet) at the moment,  , when the penny is dropped, , when the penny is dropped,
 = the initial velocity (in feet/second) of the penny at = the initial velocity (in feet/second) of the penny at  (since it was "dropped", it was not thrown up or down with any initial velocity). (since it was "dropped", it was not thrown up or down with any initial velocity).
We will use the acceleration of gravity in 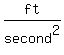 , to agree with the other units: , to agree with the other units:
 = acceleration of gravity in = acceleration of gravity in 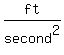 . .
Substituting, we get
 ---> --->
1a. For  , ,  , ,
so the height of the penny after three seconds is  . .
1b. When the penny hits the ground,  . Then, . Then,
 ---> ---> ---> ---> ---> ---> ---> ---> ---> ---> , ,
so the penny hits the ground after about  . .
For the second problem we will set:
 = time from the moment the ball is tossed (we will measure it in seconds, because it will be a short time), = time from the moment the ball is tossed (we will measure it in seconds, because it will be a short time),
 = the initial velocity (in meters/second) of the ball at = the initial velocity (in meters/second) of the ball at  (since it was "dropped", it was not thrown up or down with any initial velocity). (since it was "dropped", it was not thrown up or down with any initial velocity).
 (as I originally misread) (as I originally misread)  = height (in meters) at the moment, = height (in meters) at the moment,  , when the ball is tossed, , when the ball is tossed,
We will use the acceleration of gravity in  , to agree with the other units: , to agree with the other units:
 = acceleration of gravity in = acceleration of gravity in  . .
Substituting, we get
 ---> --->
2. For  , ,
 --> --> --> --> --> --> , ,
so the height of the ball after three seconds is  . .
2b. When the ball hits the ground,  . Then, . Then,
 . .
Solving the quadratic equation we get two solutions, but the negative solution does not make sense, and needs to be discarded.
So, 


 , ,
so the ball hits the ground after about  . .
 it was really meant as it was really meant as  = height (in feet), = height (in feet),
we have a units mismatch.
We have to get everything in feet, or everything in meters.
Since I am a supporter of the SI system of units, I will convert 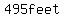 to meters. to meters.
 (rounded), so (rounded), so
 = height (in meters) at the moment, = height (in meters) at the moment,  , when the ball is tossed, , when the ball is tossed,
We will use the acceleration of gravity in  , to agree with the other units: , to agree with the other units:
 = acceleration of gravity in = acceleration of gravity in  . .
Substituting, we get
 ---> --->
2. For  , ,
 --> --> --> --> --> --> , ,
so the height of the ball after three seconds is  . .
2b. When the ball hits the ground,  . Then, . Then,
 . .
Solving the quadratic equation we get two solutions, but the negative solution does not make sense, and needs to be discarded.
So, 


 , ,
so the ball hits the ground after about  . .
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! note when dropping an object from height, the initial velocity vo is 0. G is 16 for this problem, since given values are in feet.
*********************************************************************************
1a) h(3) = -8*3^2 + 0*3 + 1250 = 1178
after 3 seconds, the penny is 1178 feet above the ground
1b) 0 = -8t^2 +1250
t^2 = 156.25 and t = 12.5
after 12.5 seconds, the penny hits the ground
*******************************************************************************
the height of the building is given in feet, so convert vo = 10 m to feet/s, vo = 32.8 feet
2a) h(3) = -8*3^2 + 32.8*3 + 495 = 521.4
after three seconds, the ball is 521.4 feet above the ground.
2b) 0 = -8t^2 + 32.8t + 495
t^2 -4.1t - 61.875 = 0
t^2 -4.1t = 61.875
t^2 -4.1t + 4.2025 = 4.2025 + 61.875
(t - 2.05)^2 = 66.0775
t - 2.05 = 8.128806801 = approx 10.2
in 10.2 seconds the ball hits the ground
****************************************************************************
here is the graph of 2b

|
|
|