Question 1005457: Suppose that a cyclist began a 279 mi ride across a state at the western edge of the state, at the same time that a car traveling toward it leaves the eastern end of the state. If the bicycle and car met after 4.5 hours and the car traveled 35.8 mph faster than the bicycle, find the average rate of each.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  = average speed of the bicycle, in mph. = average speed of the bicycle, in mph.
So,
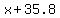 = average speed of the car, in mph, = average speed of the car, in mph,
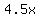 = distance covered by the bicycle in 4.5 hours, in miles, = distance covered by the bicycle in 4.5 hours, in miles,
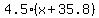 = distance covered by the car in 4.5 hours, in miles, and = distance covered by the car in 4.5 hours, in miles, and
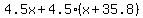 = total distance covered by the bicycle and car in 4.5 hours, in miles. = total distance covered by the bicycle and car in 4.5 hours, in miles.
Since after 4.5 hours the whole  miles of road across the state had been covered between bicycle and car, miles of road across the state had been covered between bicycle and car,
 is our equation. is our equation.
Solving:









|
|
|