SOLUTION: the perimeter of a rhombus is 120 ft. and one of its diagonal has a length of 40 ft. find the area of the rhombus?

Algebra ->  Rectangles -> SOLUTION: the perimeter of a rhombus is 120 ft. and one of its diagonal has a length of 40 ft. find the area of the rhombus?      Log On


   

Question 1005087: the perimeter of a rhombus is 120 ft. and one of its diagonal has a length of 40 ft. find the area of the rhombus?
Answer by AnlytcPhil(1806) About Me  (Show Source):
You can put this solution on YOUR website!
The rhombus looks like the figure below.  Since its perimeter 
is 120 ft., each equal length side is 120/4 = 30 ft.



We draw the other diagonal in red, which bisects the 
green 40 ft. diagonal into two 20 ft. line segments.



So the rhombus consists of 4 right triangles, so we
find the area of one of them and multiply by 4. Here is
just one of them:



We use the Pythagorean theorem to find its height,
We know its base is b=20 and its hypotenuse is 30,
we find a, the green height:

a%5E2%2Bb%5E2=c%5E2
a%5E2%2B20%5E2=30%5E2
a%5E2%2Bb%5E2=900
a%5E2=500
a=sqrt%28500%29
a=sqrt%28100%2A5%29
a=10sqrt%285%29

The area of the above right triangle is given by 
the formula:

A=expr%281%2F2%29%2Abase%2Aheight
A=expr%281%2F2%29%2A20%2A10sqrt%285%29
A=100sqrt%285%29

So the area of the rhombus is 4 times that or

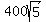answer = 400sqrt%285%29, or about 894.427191 sq. ft.

Edwin