|
Question 1005059: Find the point on each median that is two thirds of the distance from the vertex to the midpoint of the opposite side. If the vertices are A (4,-4) B (10,4) & C (2,6)
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Three medians of a triangle (of any triangle!) intersect in one common point.
It is very well known property of medians of a triangle.
In other words, three medians of a triangle are concurrent.
Regarding this property, see, for example the lesson Medians of a triangle are concurrent in this site.
It is known fact also that the intersection point divides each median in proportion 2:1 counting
from the corresponding vertex to the opposite side.
So, your problem is talking about the intersection point of the medians of the given triangle.
This point has one more remarkable property/feature: it is the centroid, or the center of mass of a triangle.
Its coordinates are
 = = 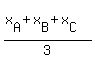 , ,
 = = 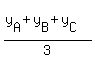 , ,
where x{A], x[B] and x[C] are x-coordinates of the triangle vertices, while y{A], y[B] and y[C] are their y-coordinates.
See the lesson The Centroid of a triangle is the Intersection point of its medians in this site.
So, for the given triangle
 = = 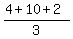 = = 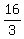 , ,
 = = 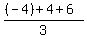 = =  . .
|
|
|
| |