Question 1004909: log3(2x-3)-log3(x+2)=3
PLEASE HELP!
Found 2 solutions by fractalier, KMST:
Answer by fractalier(6550)   (Show Source): (Show Source):
You can put this solution on YOUR website! Using the laws of exponents
log3(2x-3)-log3(x+2)=3
becomes
log(3) ((2x-3)/(x+2)) = 3
Now exponentiate 3-to-the and get
(2x-3)/(x+2) = 27
Now multiply by x+2 and solve
2x - 3 = 27x + 54
-57 = 25x
x = -57/25
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Logarithm of a quotient is the difference of the logarithms, so
 ---> --->
Logarithm of something is the exponent you have to apply the base to get that something, so if there is a solution,
 ---> ---> ---> ---> . .
The rest is simple algebra:
 ---> ---> ---> ---> ---> ---> ---> ---> ---> ---> ---> --->
The problem is that with  , ,  , ,
and logarithm of a negative number is undefined.
So, there are   . .
We could have started with "there are no solutions with
 <---> <---> <---> <---> ". ".
For 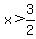 both logarithms exist, and both logarithms exist, and  . .
Then, if you were in calculus class (and even if you weren't),
you would realize that in the domain of that function
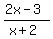 increases with increases with  , and , and
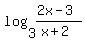 increases with increases with 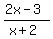 , so , so
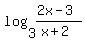 increases with increases with  , and , and
 , ,
so 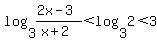 . .
Graphing 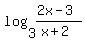 and and 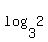 we get we get

|
|
|