Question 1004872: If a charter bus operator requires a minimum of 20 passengers and charges $60 each, determine the number of passengers that would yield maximum revenue if, to increase the passenger over 20; for example, with 22 passengers, the ticket price for each would be 60- (1.50)(22-20)=57
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! If a charter bus operator requires a minimum of 20 passengers and charges $60 each,
determine the number of passengers that would yield maximum revenue if, to increase the passenger over 20;
for example, with 22 passengers, the ticket price for each would be 60- (1.50)
(22-20)=57
:
The way I understand this, "For every $1.50 decrease, you have a 1 passenger increase
let x = the no. of $1.50 decreases from $60 and no. of passenger increases over 20
Revenue = (60-1.50x)(20+x)
FOIL
R(x) = 1200 + 60x - 30x - 1.5x^2
A quadratic equation
R(x) = -1.5x^2 + 30x + 1200
The max revenue occurs at the axis of symmetry; x = -b/(2a); a=-1.5, b=30
x = 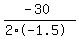
x = +10 for max revenue
:
The the fare is 60 - 10(1.5) = $45
Passenger 20 + 10 = 30
Max Revenue: 30 * $45 = $1350
|
|
|