|
Question 1004833: The vertices of a triangle are A (4,-4), B (10,4) and C (2,6). Find the distance from the vertex to the midpoint of the opposite side
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! given:
The vertices of a triangle are:
A ( , , ), B ( ), B ( , , ) and C ( ) and C ( , , ) )
plot the points and draw a triangle:

if the vertex  , the opposite side is , the opposite side is 
so, find the midpoint of the opposite side 
| Solved by pluggable solver: Midpoint |
The first point is (x1,y1). The second point is (x2,y2)
Since the first point is (4, -4), we can say (x1, y1) = (4, -4)
So  , , 
Since the second point is (10, 4), we can also say (x2, y2) = (10, 4)
So  , , 
Put this all together to get:  , ,  , ,  , and , and 
----------------------------------------------------------------------------------------
Finding the x coordinate of the midpoint: Add up the corresponding x coordinates x1 and x2 and divide that sum by 2
X Coordinate of Midpoint = 
X Coordinate of Midpoint = 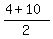
X Coordinate of Midpoint = 
X Coordinate of Midpoint = 
So the x coordinate of the midpoint is 7
----------------------------------------------------------------------------------------
Finding the y coordinate of the midpoint: Add up the corresponding y coordinates y1 and y2 and divide that sum by 2
Y Coordinate of Midpoint = 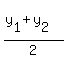
Y Coordinate of Midpoint = 
Y Coordinate of Midpoint = 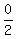
Y Coordinate of Midpoint = 
So the y coordinate of the midpoint is 0
===============================================================================
Summary:
The midpoint of the segment joining the two points (4, -4) and (10, 4) is (7, 0).
So the answer is (7, 0)
|
the midpoint is at ( , , ) and C is at ( ) and C is at ( , , ) )
find the distance between these two points:
| Solved by pluggable solver: Distance Formula |
The first point is (x1,y1). The second point is (x2,y2)
Since the first point is (7, 0), we can say (x1, y1) = (7, 0)
So  , , 
Since the second point is (2, 6), we can also say (x2, y2) = (2, 6)
So  , , 
Put this all together to get:  , ,  , ,  , and , and 
--------------------------------------------------------------------------------------------
Now use the distance formula to find the distance between the two points (7, 0) and (2, 6)

 Plug in Plug in  , ,  , ,  , and , and 




==========================================================
Answer:
The distance between the two points (7, 0) and (2, 6) is exactly  units units
The approximate distance between the two points is about 7.81024967590665 units
So again,
Exact Distance:  units units
Approximate Distance: 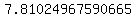 units units
|
|
|
|
| |