SOLUTION: Please help! I have already done most of the work. Recently I asked about finding all real numbers in the interval [0, 2pi] that satisfy the equation. I have worked through th

Algebra ->  Trigonometry-basics -> SOLUTION: Please help! I have already done most of the work. Recently I asked about finding all real numbers in the interval [0, 2pi] that satisfy the equation. I have worked through th      Log On


   

Question 1004805: Please help! I have already done most of the work.
Recently I asked about finding all real numbers in the interval [0, 2pi] that satisfy the equation.
I have worked through the problem but I feel like I have gotten stuck in some places. Here's the problem and where I'm at. Thank you in advance for your help!
+3+sec%5E2x+tanx+=+4+tanx+
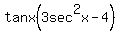
= +tanx+%283+sec%5E2x+-+4%29+
= +tanx+=+0+ and +3+sec%5E2x+-+4%29+=+0+.
Starting first with +tanx+=+0+.
= +x+=+tan%5E-1+%280%29+
= +x+=+0+
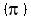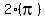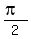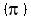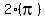Now, I've seen other examples that use +tanx+=+0+ and have the results be 0, as well as +%28pi%29+ and +2%28pi%29+ ...but I'm not quite sure why those last two should or shouldn't be included...why not +%28pi%29+%2F+2+ or +3+%28pi%29+%2F+2+ ? If you divide their sin by their cosine, doesn't it equal zero? So why choose +%28pi%29+ and +2%28pi%29+ with the zero and not others? 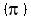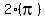Should I just leave it at 0, or should I include +%28pi%29+ and +2%28pi%29+ ?
Moving on to +3+sec%5E2x+-+4%29+=+0+.
= +%283+sec%5E2x%29+=+4+
= +%28+sec%5E2+%28x%29%29+=+%284+%2F+3%29+
= +secx+=+sqrt%284+%2F+3%29+
= +secx+=+sqrt%2812%29+%2F+3+
= +x+=+sec%5E-1+%28sqrt%2812%29+%2F+3%29+
But now where do I go? Not quite sure how to find the arcsecant of something with a square root...How do I type that into my calculator? (I dont have a graphing calculator...but I can do sines, cosines and tangents with their inverses).
Help would be greatly appreciated. Thank you! :)
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
1.  Regarding first part of your question.

You got 

tan(x) = 0. 

The solutions of this equation are  x = 0, +/-pi, +/-2pi, +/-3pi , . . . , +/-k%2Api, . . . .

Of them,  only 0, pi and 2pi  belong to the segment  [0, 2pi]  that you pointed.

Other values that you are asking about,  like pi%2F2, 3pi%2F2,  are not the roots of the equation  tan(x) = 0.


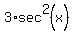2.  Moving on to  3%2Asec%5E2%28x%29 - 4 = 0.

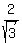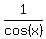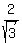It is  sec%28x%29 = +/-2%2Fsqrt%283%29,     or     1%2Fcos%28x%29 = +/-2%2Fsqrt%283%29     or     cos(x) = +/-sqrt%283%29%2F2.

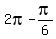If  cos(x) = sqrt%283%29%2F2,  then x = pi%2F6 and x = 2pi+-+pi%2F6 = 11pi%2F6 are the solutions in the segment  [0, 2pi].

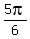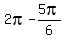If  cos(x) = -sqrt%283%29%2F2,  then x = 5pi%2F6 and x = 2pi+-+5pi%2F6 = 7pi%2F6 are the solutions in the segment  [0, 2pi].


I recommend you to make a sketch of the unit circle, to mark the angles 0°, 30°, 45°, 60° and 90° in it and to write 

the values of sin, cos and tan for these angles.

Then mark all other angles like 120°, 135°, 150°, 180° and so on till 360° and do the same.

After that you will be much more confident in such problems.