Question 1004512: Three numbers whose sum is 3 form an arithmetic sequence and their squares form a geometric sequence. What are the numbers?
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Three numbers whose sum is 3 form an arithmetic sequence and their squares form a geometric sequence.
What are the numbers?
----------------------------------------------------------------
Answer. The numbers are 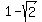 , ,  , and , and  . .
Solution
Since three numbers form an arithmetic progression, we can represent them as (a-d), a, and (a+d),
where a is the middle term and d is the common difference.
The squares of these numbers are  , ,  , and , and 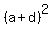 . .
The fact that the squares form a geometric progression means that
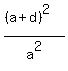 = = 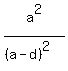 (1) (1)
(the ratio of the third to the second is equal to the ratio of the second to the first, as these ratios are
the common ratio of the geometric progression). The formula (1) implies, after simplifying, that
 = = 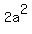 , or d = a , or d = a . .
Next, since the sum of the tree numbers is 3, we conclude that
(a-d) + a + (a+d) = 3a = 3, and, hence, a = 1. In turn, it means that d =  . .
Thus our sequence of three numbers is 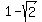 , 1, and , 1, and  . .
As a check, it is clear that the found numbers form arithmetic progression and their sum is 3.
Their squares are 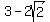 , 1, and , 1, and 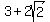 . .
The consequtive ratios of the squares are 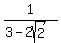 and and 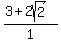 . .
Finally, you can check yourself that these ratios are equal, which means that the squares form
the geometric progression.
The solution is completed.
Thank you for submitting the fresh, sweet and crispy problem!
|
|
|