Find the equation of the tangent line to the curve


 at the point (4,1).
at the point (4,1).


 We take the derivative implicitly:
We take the derivative implicitly:


 Substitute (x,y) = (4,1)
Substitute (x,y) = (4,1)
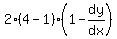


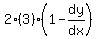





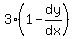







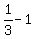








 The derivative at a point is the slope of the
line tangent to the curve at the point, therefore
the slope of the tangent line is
The derivative at a point is the slope of the
line tangent to the curve at the point, therefore
the slope of the tangent line is


 We use the point-slope formula for the equation
of the tangent line:
We use the point-slope formula for the equation
of the tangent line:
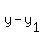

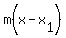 where (x1,y1) = (4,1)
[Do not substitute for x and y, but leave them
as variables]
where (x1,y1) = (4,1)
[Do not substitute for x and y, but leave them
as variables]











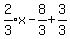


 , graphed in green below:
, graphed in green below:
 Edwin
Edwin