|
Question 1003709: Working together, it takes Sam, Jenna, and Frank two hours to paint one room. When Sam is working alone, she can paint one room in 6 hours. When Jenna works alone, she can paint one room in four hours.
Determine how long it would take Frank to paint one room on his own.
Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website! Working together, it takes Sam, Jenna, and Frank two hours to paint
one room. When Sam is working alone, she can paint one room in 6
hours. When Jenna works alone, she can paint one room in four
hours.
When Sam is working alone, she can paint one room in 6 hours.
Since Sam can paint 1 room in 6 hours, her painting rate is
1 room per 6 hours 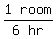or  or
When Jenna works alone, she can paint one room in four hours.
Since Jenna can paint 1 room in 4 hours her painting rate is
1 room per 4 hours 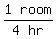or  or
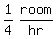
Determine how long it would take Frank to paint one room on his own.
Suppose that when Frank works alone, he can paint one room in x hours.
Since Frank can paint 1 room in x hours, his painting rate is
1 room per x hours 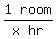or  or
Working together, it takes Sam, Jenna, and Frank two hours to paint
one room.
Since all three working together can paint 1 room in 2 hours, the sum
of their painting rates is 1 room per 2 hours
or  or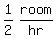 
So the equation comes from that fact, that the sum of their painting
rates is :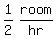
 
   
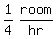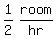
Multiply through by LCD 12x
   
So it will take Frank 12 hours to paint a room by himself.
Edwin
|
|
|
| |
